DA0-001 CompTIA Data+ Certification Exam Questions and Answers

This is because a logical function is a type of function that returns a value based on a condition or a set of conditions. A logical function can be used to generate the data in the Sales_indicator column by comparing the values in the Sales column with a threshold of $50,000 and returning either “Exceeded $50,000” or “Not exceeded $50,000” accordingly. For example, a logical function in Excel that can achieve this is:

The other functions are not suitable for generating the data in the Sales_indicator column. Here is why:

Aggregate is a type of function that performs a calculation on a group of values, such as sum, average, count, etc. An aggregate function cannot generate the data in the Sales_indicator column because it does not compare the values in the Sales column with a threshold or return a text value based on a condition.

Date is a type of function that manipulates or extracts information from dates, such as year, month, day, etc. A date function cannot generate the data in the Sales_indicator column because it does not use the values in the Sales column or return a text value based on a condition.

Sort is a type of function that arranges the values in a column or a range in ascending or descending order. A sort function cannot generate the data in the Sales_indicator column because it does not create a new column or return a text value based on a condition.

The option that is a common data analytics tool that is also used as an interpreted, high-level, general-purpose programming language is Python. Python is a popular and versatile programming language that can be used for various purposes, such as web development, software development, automation, machine learning, and data analysis. Python has many features and libraries that make it suitable for data analytics, such as its simple syntax, dynamic typing, multiple paradigms, built-in data structures, NumPy, pandas, matplotlib, scikit-learn, etc. The other options are not programming languages, but software applications or platforms that are used for data analytics or related tasks. SAS is a software suite that provides advanced analytics, business intelligence, data management, and predictive analytics capabilities. Microsoft Power BI is a business analytics service that provides interactive visualizations and business intelligence capabilities. IBM SPSS is a software package that offers statistical analysis, data mining, text analytics, and predictive analytics capabilities. Reference: Python For Data Analysis - DataCamp

Explanation

1. Duplicates

2. Misspellings

The most common data quality issues are difficult to resolve in Excel because of their rigidity. It forces analysts to do a ton of manual work, which results in a high probability of an error being introduced to the data set. Those common issues include:

- Blanks

- Nulls

- Outliers

- Duplicates

- Extra spaces

- Misspellings

- Abbreviations and domain-specific variations

- Formula error codes

When introduced, these errors can skew or even invalidate the resulting analysis. A smart tool would minimize the possibility of error by automating the manual work. In Excel, you might look for data quality issues in one of two ways. First, you might use auto filters on specific columns to scan for anomalies and blanks or you might use a pivot table to find gaps and discrepancies.

In either case, you're scanning for the anomalies yourself. Suffice it to say that's not a very efficient process. It also means accuracy is only as good as the analyst's eye, so the probability of error varies throughout the day.

This is because inconsistency is a type of data quality issue that occurs when the data does not follow a common format, structure, or rule across different sources or systems, which can affect the efficiency and performance of the analysis or process. Inconsistency can be caused by having different spellings, punctuations, capitalizations, or abbreviations for the same or similar values in a data set, such as “M”, “m”, “Male”, or “male” for gender in this case. Inconsistency can be eliminated or reduced by using data cleansing techniques, such as standardizing or normalizing the data values. The other options are not correct descriptions of the data set. Here is why:

• Data bias is a type of data quality issue that occurs when the data is not representative or proportional of the population or the parameter, which can affect the validity and reliability of the analysis or process. Data bias can be caused by having a sample that is too small, too large, or too skewed for the population or the parameter, such as having only male customers for a product that targets both genders in this case. Data bias can be eliminated or reduced by using sampling techniques, such as stratified or cluster sampling.
• The data is incomplete is a type of data quality issue that occurs when the data is absent or missing in a data set, which can affect the accuracy and reliability of the analysis or process. The data is incomplete can be caused by various factors, such as human error, system error, or non-response. The data is incomplete can be addressed by using various methods, such as replacing or imputing the missing values with some reasonable estimates, such as mean, median, mode, or regression.
• The data is outliers is a type of data quality issue that occurs when the data has values that are unusually high or low compared to the rest of the data set, which can affect the quality and validity of the analysis or process. The data is outliers can be caused by various factors, such as measurement error, natural variation, or extreme events. The data is outliers can be addressed by using various methods, such as removing or filtering out the outliers, or using robust statistics that are less sensitive to outliers, such as median, interquartile range, or box plot.

The mean height for the five dogs is calculated by adding up all the heights and dividing by the number of dogs. The formula is:

mean = (300 + 430 + 170 + 470 + 600) / 5 mean = 1970 / 5 mean = 394

Therefore, option A is correct.

Option B is incorrect because it is the median height, which is the middle value when the heights are arranged in ascending order.

Option C is incorrect because it is the mean height multiplied by 1.25.

Option D is incorrect because it is the mean height multiplied by 1.28.

Merging tables to create a master file that includes all transactions for both online and in-store sales is best described as data consolidation. This process involves combining data from various sources into a single, unified dataset. Data consolidation is essential for providing a comprehensive view of all transactions, which can be used for analysis, reporting, and decision-making purposes.

References: The answer is based on standard data management practices and the definition of data consolidation. No specific external documents were referenced for this response.

The option that the data analyst should use to best communicate the information to the manager is a summary with statistics, conclusions, and recommendations from the data analyst. A summary is a concise and clear way of presenting the main findings and insights from the data analysis report. A summary should include relevant statistics that support the conclusions and recommendations from the data analyst. A summary should also highlight the most important KPIs and measure the return on marketing investment in relation to the objectives of the online marketing campaign. The other options are not as effective as using a summary to communicate the information to the manager, as they either provide too much or too little information or do not address the manager’s needs or expectations. A real-time monitor may provide too much information that can be overwhelming or distracting for the manager who wants to see only the most important KPIs and measure the return on marketing investment. A self-service dashboard may provide too little information that can be insufficient or unclear for the manager who wants to see some guidance and interpretation from the data analyst. A spreadsheet of raw data may provide irrelevant or inaccurate information that can be confusing or misleading for the manager who wants to see some analysis and insights from the data analyst. Reference: [How to Write an Executive Summary for Your Data Analysis Report - Towards Data Science]

The logical statement that results in Table B is Option D. Option D is a logical statement that uses the AND operator to combine two conditions: Name = “Tom” and Region = “BC”. The AND operator returns true only if both conditions are true, otherwise it returns false. Therefore, Option D will select only the rows from Table A that satisfy both conditions, which are rows 4, 5, 6, and 7. These rows form Table B, as shown below:

Name | Gender flag | Level | College | Code | Region Tom | Male | Elementary | A | BC | BC Kim | Female | Elementary | A | BC | BC Pat | Female | Elementary | A | BC | BC Ben | Male | Elementary | A | BC | BC

The other options are not correct, as they use different logical operators or conditions that do not result in Table B. Option A uses the OR operator, which returns true if either condition is true, or both. Option A will select all the rows from Table A except row 3, which does not match either condition. Option B uses the NOT operator, which returns the opposite of the condition. Option B will select all the rows from Table A except rows 4, 5, 6, and 7, which match the condition. Option C uses a different condition, Region = “ON”, which does not match any row in Table A. Option C will select no rows from Table A. Reference: [SQL Logical Operators - W3Schools]

A credit card number is an example of structured data, which is a type of data that conforms to a data model, has a well-defined structure, follows a consistent order, and can be easily accessed and used by a person or a computer program. A credit card number consists of 16 digits that are divided into four groups of four digits each, separated by spaces or hyphens. The first six digits indicate the issuer identification number, the next nine digits indicate the account number, and the last digit is a check digit that validates the number. A credit card number can be stored and processed in a structured format, such as a database or a spreadsheet1.

The invalid data type is the best description for the issue in which character values are mixed with integer values in a data set column. Invalid data type means that the data does not match the expected or required format or structure for a given variable or attribute. For example, if a column is supposed to store numerical values, but some rows contain text values, then those rows have an invalid data type. References: CompTIA Data+ Certification Exam Objectives, page 10

A dynamic report is a type of report that shows data that changes or updates automatically based on certain criteria or parameters. A dynamic report can allow users to interact with the data, filter it, drill down into it, or visualize it in different ways. A dynamic report is suitable for situations where the data changes frequently or where real-time or near-real-time data is needed for decision making or analysis. In this case, the data analyst is asked to create a sales report for the second-quarter 2020 board meeting, which will include a review of the business’s performance through the second quarter. The board meeting will be held on July 15, 2020, after the numbers are finalized. This means that the data analyst does not need to show real-time or dynamic data, but rather a fixed and accurate view of the sales data for the second quarter. Therefore, a static report would be the best way to meet this stakeholder requirement. Therefore, the correct answer is A. References: [What are Dynamic Reports? | Sisense], Static vs Dynamic Reports - What’s The Difference? | datapine

This is because a scatter plot is a type of chart that shows the relationship between two variables for each observation or unit in a data set, such as study hours and exam scores for each student in this case. A scatter plot can be used to display and analyze the correlation, trend, or pattern among the variables, as well as identify any outliers or clusters in the data. For example, a scatter plot can show if there is a positive, negative, or no correlation between study hours and exam scores, as well as show if there are any students who have unusually high or low exam scores compared to their study hours. The other charts are not the best charts to represent the relationship between the variables. Here is why:

• A histogram is a type of chart that shows the frequency or the count of values in a single variable for different intervals or bins, such as exam scores for different ranges in this case. A histogram can be used to display and analyze the distribution, shape, or spread of the variable, as well as identify any gaps, peaks, or skewness in the data. For example, a histogram can show if most students have high, low, or average exam scores, as well as show if there are any intervals that have no students at all.
• A heat map is a type of chart that shows the intensity or the magnitude of values in two variables for different categories or groups, such as exam scores and study hours for different student names in this case. A heat map can be used to display and analyze the variation, contrast, or comparison among the categories or groups, as well as identify any hot spots, cold spots, or gradients in the data. For example, a heat map can show which students have higher or lower exam scores and study hours than others, as well as show if there is a color pattern that indicates a relationship between exam scores and study hours.
• A bar chart is a type of chart that shows the value or the amount of a single variable for different categories or groups, such as exam scores for different student names in this case. A bar chart can be used to display and analyze the comparison, ranking, or proportion among the categories or groups, as well as identify any differences, similarities, or outliers in the data. For example, a bar chart can show which students have higher or lower exam scores than others, as well as show if there are any students who have exceptionally high or low exam scores.

This is because link analysis is a type of analysis that determines whether the data being analyzed is connected to other datapoints, such as entities, events, or relationships. Link analysis can be used to identify and visualize the patterns, networks, or associations among the datapoints, as well as measure the strength, direction, or frequency of the connections. For example, link analysis can be used to determine if there is a connection between a customer’s purchase history and their loyalty program status. The other types of analysis are not the best types of analysis to conduct to determine whether the data being analyzed is connected to other datapoints. Here is why:

• Trend analysis is a type of analysis that determines whether the data being analyzed is changing over time, such as increasing, decreasing, or fluctuating. Trend analysis can be used to identify and visualize the patterns, cycles, or movements in the data points, as well as measure the rate, direction, or magnitude of the changes. For example, trend analysis can be used to determine if there is a change in a company’s sales revenue over a period of time.
• Performance analysis is a type of analysis that determines whether the data being analyzed is meeting certain goals or objectives, such as targets, benchmarks, or standards. Performance analysis can be used to identify and visualize the gaps, deviations, or variations in the data points, as well as measure the efficiency, effectiveness, or quality of the outcomes. For example, performance analysis can be used to determine if there is a gap between a student’s test score and their expected score based on their previous performance.
• Exploratory analysis is a type of analysis that determines whether there are any insights or discoveries in the data being analyzed, such as patterns, relationships, or anomalies. Exploratory analysis can be used to identify and visualize the characteristics, features, or behaviors of the data points, as well as measure their distribution, frequency, or correlation. For example, exploratory analysis can be used to determine if there are any outliers or unusual values in a dataset.

To compare the students’ scores, we need to standardize them by using the z-score formula, which is:

z = (x - μ) / σ

where x is the raw score, μ is the mean, and σ is the standard deviation. The z-score tells us how many standard deviations a score is above or below the mean. A higher z-score means a better score relative to the average.

Using the table, we can calculate the z-scores for each student as follows:

Randy: z = (76 - 70) / 2 = 3 Katie: z = (86 - 80) / 3 = 2 Ralph: z = (80 - 75) / 2 = 2.5 Jean: z = (80 - 90) / 1 = -10

The student with the highest z-score is Randy, with a z-score of 3. This means that Randy scored 3 standard deviations above the mean in math, which is the best performance among the four students. Therefore, the correct answer is A.

References: Comparing with z-scores (video) | Z-scores | Khan Academy, 17 Important Data Visualization Techniques | HBS Online

When dealing with multiple date columns from different data sources, it’s crucial to ensure consistency and accuracy in the dataset. The best practice is to merge the date columns and standardize the date format across the entire dataset. This approach helps maintain data integrity, simplifies analysis, and avoids confusion that could arise from having multiple date formats. Unifying the date format is particularly important when the data will be used for time series analysis or when dates are key to joining with other datasets.

References:

• Best practices in data merging emphasize the importance of a single point of reference and the need to avoid data loss or damage to individual data structures1.
• Power BI guides suggest that merging columns should be done carefully to maintain data integrity and avoid errors and inconsistencies2.
• Oracle Blogs highlight the need for a consistent number of columns among data sources when combining data with unions3.
• Excel tutorials recommend organizing data before merging and using formulas for complex merges4.
• An Excel guide on merging date and time columns advises employing functions to ensure seamless handling of non-date values5.

A summary with statistics, conclusions, and recommendations from the data analyst is the best way to communicate the results of an online marketing campaign to the marketing manager. A summary can provide a concise and clear overview of the most important KPIs and measure the return on marketing investment, as well as highlight the main findings and insights from the data analysis. A summary can also include actionable suggestions and best practices for improving the campaign performance and achieving the marketing objectives. A summary is different from other options, such as a real-time monitor, a self-service dashboard, or a spreadsheet of raw data, which may not provide enough context, interpretation, or guidance for the manager. Therefore, the correct answer is D. References: How to Write a Data Analysis Report: 6 Essential Tips, How to Write a Marketing Report (with Pictures) - wikiHow

 Alphanumeric values are values that contain both letters and numbers, such as A3J7. The other options are numeric values, as they contain only numbers, such as 10.1E2, 13.6, and 1347. Reference: Guide to CompTIA Data+ and Practice Questions - Pass Your Cert

Explanation

The best answer is to use a watermark to identify the report as a draft. A watermark is a faint image or text that appears behind the content of a document, indicating its status or ownership. By using a watermark, Kelly can clearly communicate that the report is not final and still subject to changes or feedback. This can prevent confusion among the readers and avoid any misuse or misinterpretation of the report. The other options are not as effective as using a watermark, as they either do not indicate the status of the report or do not reach the appropriate stakeholders. Distributing the report via email or publishing it on an internally facing website may not make it clear that the report is a draft and may cause confusion or errors. Showing the report to her immediate supervisor may not get enough feedback from other relevant stakeholders who may have different perspectives or insights. Reference: How to Add a Watermark in Microsoft Word - Lifewire

Short explanation: Logical functions are the most appropriate to use for categorizing data into bands, because they allow the data analyst to apply conditional statements and criteria to the data values. For example, the IF function can be used to assign a band name based on whether a value meets a certain condition or not. Other logical functions that can be useful for categorizing data are AND, OR, NOT, and IFERROR12

The correct join the analyst should complete is B. LEFT JOIN, four rows.

A LEFT JOIN is a type of SQL join that returns all the rows from the left table, and the matched rows from the right table. If there is no match, the right table will have null values. A LEFT JOIN is useful when we want to preserve the data from the left table, even if there is no corresponding data in the right table1

Using the example tables, a LEFT JOIN query would look like this:

SELECT t1.Name, t1.City, t2.Age FROM Table1 t1 LEFT JOIN Table2 t2 ON t1.Name = t2.Name;

The result of this query would be:

Name City Age Jane Smith Detroit NULL John Smith Dallas 34 Candace Johnson Atlanta 45 Kyle Jacobs Chicago 39

As you can see, the query returns four rows, one for each name in Table1. The name John Smith appears twice in Table2, but only one of them is matched with the name in Table1. The name Jane Smith does not appear in Table2, so the age column has a null value for that row.

Parsing is the data manipulation technique that should be used to separate the column into multiple columns for each component of the name. Parsing is the process of breaking down a string of text into smaller units, such as words, symbols, or numbers. Parsing can be used to extract specific information from a text column, such as names, addresses, phone numbers, etc. Parsing can also be used to split a text column into multiple columns based on a delimiter, such as a comma, space, or dash1. In this case, the analyst can use parsing to split the column by the comma delimiter and create three new columns: one for the last name, one for the first name, and one for the middle initial. This will make the data more organized and easier to analyze.

Explanation

Simply put, a z-score (also called a standard score) gives you an idea of how far from the mean a data point is. But more technically it's a measure of how many standard deviations below or above the population mean a raw score is. A z-score can be placed on a normal distribution curve.

This is a simulation question that requires you to create a dashboard with visualizations that meet the director’s needs. Here are the steps to complete the task:

• Drag and drop the visualization that shows the county outages on the top left space of the dashboard. This visualization is a map of the state with different colors indicating the number of outages in each county. You can choose any color scheme that suits your preference, but make sure that the colors are consistent and clear. For example, you can use a gradient of red to show the counties with more outages and green to show the counties with less outages.
• Drag and drop the visualization that shows the status of the outages on the top right space of the dashboard. This visualization is a pie chart that shows the percentage of outages that are active, restored, or pending. You can choose any color scheme that suits your preference, but make sure that the colors are distinct and easy to identify. For example, you can use red for active, green for restored, and yellow for pending.
• Drag and drop the visualization that shows the overall trend of outages on the bottom space of the dashboard. This visualization is a line graph that shows the number of outages over time. You can choose any color scheme that suits your preference, but make sure that the color is visible and contrasted with the background. For example, you can use blue for the line and white for the background.
• Select appropriate titles and labels for each visualization. Titles and labels may be used more than once. For example, you can use “County Outages” as the title for the map, “Status” as the title for the pie chart, and “Trend” as the title for the line graph. You can also use “County”, “Number of Outages”, “Active”, “Restored”, “Pending”, “Time”, and “Number of Outages” as labels for the axes and legends of the visualizations.

Explanation

The correct answer is: 60

Range is the interval between the highest and the lowest score.

Range is a measure of variability or scatteredness of the varieties or observations among themselves and does not give an idea about the spread of the observations around some central value.

Symbolically R = Hs - Ls.

Where R = Range; Hs is the 'Highest score' and Ls is the Lowest Score.

The scores of ten students in a test are: 17, 23, 30, 36, 45, 51, 58, 66, 72, 77.

The highest score is 77 and the lowest score is 17.

So the range is the difference between these two scores Range = 77 - 17 = 60

The measures of central tendency include the mode, median, and mean. The mode is the value that appears most frequently in a data set. In this case, the speed of 36 appears twice, making it the mode. The median is the middle value when a data set is ordered from least to greatest; for these speeds, when ordered (18, 36, 36, 38, 55, 67), the median is the average of the two middle numbers, which is ( \frac{36 + 38}{2} = 37 ). The mean is the average of all values, calculated as ( \frac{55 + 36 + 18 + 67 + 36 + 38}{6} = 41.7 ).

References:

• The calculation of the mode, median, and mean is based on standard statistical formulas and definitions.

The measures of central tendency for speed include the mode, median, and mean. To calculate these, we first need to organize the data:

• Speeds in ascending order: 18, 36, 36, 38, 55, 67
• Mode is the value that appears most frequently, which is 36, as it appears twice.
• Median is the middle value when the data is ordered. Since we have an even number of observations, we take the average of the two middle values (36 and 38), resulting in 37.
• Mean is the sum of all values divided by the number of values. (18+36+36+38+55+67)/6=41.5(18+36+36+38+55+67)/6=41.5.

Thus, the correct option is D, which includes Mode = 36, Median = 37, and Mean = 41.5. The range, maximum, and minimum values, although useful in understanding data dispersion, are not measures of central tendency and are therefore not relevant to this specific question.

The answer is A. Outlier.

Short explanation: An outlier is a data point that differs significantly from the rest of the data in a dataset. An outlier can indicate an error, an anomaly, or a rare event in the data. An outlier can affect the statistical analysis and visualization of the data, such as skewing the mean, variance, or distribution of the data. Therefore, data should be cleaned to identify and remove or correct any outliers.

The image below shows a box plot graph with a vertical axis labeled “Customer Calls” and a horizontal axis labeled “Churn”. The box plot is blue in color and the median value is around 2. There are 7 outliers above the box plot, ranging from 4 to 8.

image)

A box plot is a type of graph that can show the distribution of data values using five summary statistics: minimum, maximum, median, first quartile, and third quartile. The box represents the interquartile range (IQR), which is the difference between the first and third quartiles. The median is shown as a line inside the box. The whiskers extend from the box to the minimum and maximum values, excluding any outliers. Outliers are shown as dots or circles outside the whiskers.

In this graph, we can see that most of the customer calls are between 0 and 4, with a median of 2. However, there are 7 outliers that have more than 4 customer calls, up to 8. These outliers may indicate some customers who have more issues or complaints than others, or some errors or anomalies in the data collection or recording process. These outliers can affect the analysis and interpretation of the customer calls and churn relationship, such as making it seem that more customer calls lead to less churn, which may not be true for the majority of the customers. Therefore, data should be cleaned to investigate and handle these outliers appropriately.

Discrete data are data that can only assume specific values that are countable and distinct. For example, the number of books, the number of heads in a coin toss, or the number of patients in a hospital are discrete data. Discrete data cannot have fractional or decimal values, and there are clear spaces between the possible values12.

Continuous data are data that can assume any value within a range and can be meaningfully divided into smaller parts. For example, the weight, height, length, time, or temperature are continuous data. Continuous data can have fractional or decimal values, and there are infinite numbers of possible values between any two points12.

Customer segmentation is a type of cluster analysis, which is a method of grouping data points based on their similarities or differences. Cluster analysis can help identify patterns and trends in the data, as well as target specific groups of customers for marketing purposes. One common technique for customer segmentation is RFM analysis, which stands for recency, frequency, and monetary value. This technique assigns a score to each customer based on how recently they bought the product, how often they buy the product, and how much they spend on the product. These scores can then be used to create clusters of customers with different characteristics and preferences. Therefore, the correct answer is D. References: Cluster Analysis - Statistics Solutions, RFM Analysis: The Ultimate Guide for Customer Segmentation

The most efficient function for an analyst to execute a data pull for the two prior months would be the Date function. This function allows for the manipulation and formatting of date values within a database. Using Date functions, an analyst can dynamically calculate the start and end dates for the previous two months, ensuring that the data pull is accurate and automated without manual intervention.

For example, SQL functions like DATEADD and DATEDIFF can be used to determine the exact range of dates needed for the data pull. These functions can calculate the first and last day of the previous months relative to the current date, which is essential for monthly reporting and analysis.

References:

• Discussions on Stack Overflow suggest using SQL date functions like DATEADD and DATEDIFF to dynamically extract data for previous months, which supports the use of Date functions12.
• The use of Date functions is also recommended for ensuring that the data pull is not only efficient but also accurate, as it avoids potential errors associated with manual date entry3.

This is because an IF function is a type of logical function that returns a value based on a condition or a set of conditions. An IF function can be used to manipulate data by applying different actions or calculations depending on whether the condition is true or false. For example, an IF function in Excel that can achieve this is:

=IF (condition, value_if_true, value_if_false)

The other data manipulation techniques are not examples of logical functions. Here is why:

• WHERE is a type of clause that filters data based on a condition or a set of conditions. A WHERE clause can be used to manipulate data by selecting only the rows that satisfy the condition(s). For example, a WHERE clause in SQL that can achieve this is:

• AGGREGATE is a type of function that performs a calculation on a group of values, such as sum, average, count, etc. An AGGREGATE function can be used to manipulate data by summarizing or aggregating the values in a column or a table. For example, an AGGREGATE function in SQL that can achieve this is:

• BOOLEAN is a type of data type that represents two possible values: true or false. A BOOLEAN data type can be used to manipulate data by storing or returning logical values based on a condition or a set of conditions. For example, a BOOLEAN data type in Python that can achieve this is:

Exploratory data analysis (EDA) is a process of examining and summarizing a dataset using various techniques, such as descriptive statistics, visualizations, correlations, outliers detection, and hypothesis testing. EDA can help reveal the main characteristics, patterns, trends, and insights from the data, as well as identify any problems or issues with the data quality or structure. EDA is usually performed after understanding a business requirement for a data analysis report and before building a mock dashboard/presentation layout. Therefore, the correct answer is B. References: [What is Exploratory Data Analysis? | Definition and Examples], [Exploratory Data Analysis in Python]

Explanation

The correct answer is B: Derived variables Derived variables are variables that you create by calculating or categorizing variables that already exist in your data set.

Data merge is incorrect. Data merging is the process of combining two or more data sets into a single data set. Data blending is incorrect.

Data blending involves pulling data from different sources and creating a single, unique, dataset for visualization and analysis.

Data append is incorrect. A data append is a process that involves adding new data elements to an existing database.

Explanation

Data merging is the process of combining two or more data sets into a single data set. Most often, this process is necessary when you have raw data stored in multiple files, worksheets, or data tables, that you want to analyze all in one go.

The best answer is C. Microsoft Power BI.

Microsoft Power BI is a business analytics and business intelligence service by Microsoft. It aims to provide interactive visualizations and business intelligence capabilities with an interface simple enough for end users to create their own reports and dashboards. Power BI can connect to multiple data sources, clean and transform data, create custom calculations, and visualize data through charts, graphs, and tables. Power BI can be accessed through a web browser, mobile device, or desktop application and integrated with other Microsoft tools like Excel and SharePoint12

Python is not correct, because Python is a general-purpose programming language that can be used for various applications, including data analysis and visualization. However, Python is not a dedicated business analytics tool, and it requires coding or programming skills to create reports and dashboards.

R is not correct, because R is a programming language and software environment for statistical computing and graphics. R can be used for data analysis and visualization, but it is not a specialized business analytics tool, and it requires coding or programming skills to create reports and dashboards.

SAS is not correct, because SAS is a software suite for advanced analytics, business intelligence, data management, and predictive analytics. SAS can provide interactive visualizations and business capabilities, but it does not have an interface that is simple enough for end users to create their own reports and dashboards. SAS also requires coding or programming skills to use its features.

This is because the price of the Rose unit can be estimated using the average cost per square foot of the original floor plans, which are Jasmine, Orchid, Azalea, and Tulip. To find the average cost per square foot of the original floor plans, we can use the following formula:

Plugging in the values from the original floor plans, we get:

To find the price of the Rose unit, we can use the following formula:

Plugging in the values from the Rose unit, we get:

Therefore, the price of the Rose unit should be $705,200, using the average cost per square foot of the original floor plans.

Explanation

Data encryption can be used to translate data into another form so it can only be read by a user who has a key or a password. Data encryption is a process of transforming data using an algorithm or a cipher to make it unreadable to anyone except those who have the key or the password to decrypt it. Data encryption is a common method of protecting data from unauthorized access, modification, or theft. Reference: Guide to CompTIA Data+ and Practice Questions - Pass Your Cert

This is because a data lake is a type of storage system that stores unstructured data from different sources, such as text, images, audio, video, etc. A data lake can be used to store unstructured data from different sources by using a schema-on-read approach, which means that it does not impose any structure or format on the data when it is stored, but rather applies it when it is read or accessed. A data lake can also be used to store unstructured data from different sources by using a distributed file system, such as Hadoop, which means that it can store large volumes and varieties of data across multiple servers or nodes. The other storage systems are not used to store unstructured data from different sources. Here is why:

• A database management system is a type of software application that manages and controls databases, which are collections of structured or semi-structured data that are organized into tables, rows, and columns. A database management system is not used to store unstructured data from different sources, but rather to store structured or semi-structured data from specific sources by using a schema-on-write approach, which means that it imposes a structure or format on the data when it is stored, and requires it to follow certain rules and constraints, such as primary keys, foreign keys, or referential integrity.
• A database is a type of storage system that stores structured or semi-structured data that are organized into tables, rows, and columns. A database is not used to store unstructured data from different sources, but rather to store structured or semi-structured data from specific sources by using a relational model, which means that it establishes and maintains relationships between different tables based on common columns or keys. A database can also be used to store structured or semi-structured data from specific sources by using a query language, such as SQL, which means that it can access and manipulate the data using statements or commands.
• A data warehouse is a type of storage system that stores structured or semi-structured data that are integrated and aggregated from different sources or systems, such as databases, cloud services, or web applications. A data warehouse is not used to store unstructured data from different sources, but rather to store structured or semi-structured data from various sources by using an ETL process, which means that it extracts, transforms, and loads the data into a common format, structure, or schema. A data warehouse can also be used to store structured or semi-structured data from various sources by using an OLAP model, which means that it supports online analytical processing of the data using multidimensional cubes or queries.

A pie chart is the best choice to show the composition between the categories of the survey response data set. A pie chart represents the whole with a circle, divided by slices into parts. Each slice shows the relative size of each category as a percentage of the total. A pie chart is useful when the categories are mutually exclusive and add up to 100%. The table shows the favorite color and the number of responses for each color, which can be easily converted into percentages. A pie chart can show how each color contributes to the total number of responses.

Option A is incorrect because a histogram is used to show how data points are distributed along a numerical scale. The survey response data set is not numerical, but categorical.

Option C is incorrect because a line chart is used to show trends or changes over time. The survey response data set does not have a time dimension.

Option D is incorrect because a scatter plot is used to show the relationship between two numerical variables. The survey response data set does not have two numerical variables.

Option E is incorrect because a waterfall chart is used to show how an initial value is increased or decreased by a series of intermediate values. The survey response data set does not have an initial value or intermediate values.

References:

• How to Choose the Right Chart for Your Data - Infogram
• How to Choose the Right Data Visualization | Tutorial by Chartio
• Find the Best Visualizations for Your Metrics - The Data School
• How to choose the best chart or graph for your data

Neo4j is a type of non-relational database that uses a graph model to store data. A graph database is a database that represents data as nodes and edges, where nodes are entities and edges are relationships between them. A graph database can store complex and diverse data that is not easily structured in tables. A graph database can also perform fast and efficient queries on the data by traversing the connections between the nodes

Explanation

INSERT

The INSERT command is used to add new records to a database table.

The SELECT command is used to retrieve information from a database. It's the most commonly used command in SQL because it is used to pose queries to the database and retrieve the data that you're interested in working with.

The UPDATE command is used to modify rows in the database.

The CREATE command is used to create a new table within your database or a new database on your server.

 A FULL JOIN in SQL combines all rows from two or more tables, regardless of whether a match exists. The result includes all records when there is a match in the joined tables and fills in NULLs for missing matches on either side. Given the two tables in the image, the first table has three rows, and the second table has four rows. The FULL JOIN of these tables will include all rows from both tables, resulting in four rows. Since there are three unique columns in the first table (ID, Title) and three unique columns in the second table (ID, Name, Project_ID), with the common column being ID, the resulting table will have four columns (ID, Title, Name, Project_ID).

References:

• SQL documentation on FULL JOIN operations.

The mean is the average of all the values in a data set. To calculate the mean, we add up all the values and divide by the number of values. In this case, the mean for Q1 sales is ($2,000 + $3,000 + $4,000 + $2,500 + $3,500) / 5 = $3,082.72 References: CompTIA Data+ Certification Exam Objectives, page 9

The answer is D. Data sources and attributes.

Short explanation: The data analyst should consider the data sources and attributes first when creating a dashboard, because they determine what kind of information can be included and how it can be displayed. The data sources and attributes define the origin, quality, format, and structure of the data that will be used for the dashboard. They also affect the data refresh rate, the consumer types, and the access permissions of the dashboard12

A. Data refresh rate is not the first thing to consider, because it depends on the data sources and attributes. The data refresh rate is how often the data in the dashboard is updated or refreshed to reflect the latest changes. The data refresh rate can vary depending on the type, frequency, and availability of the data sources1

B. Consumer types are not the first thing to consider, because they depend on the data sources and attributes. The consumer types are the intended audiences or users of the dashboard, who may have different needs, preferences, and expectations for the dashboard. The consumer types can influence the design, layout, and functionality of the dashboard. However, the consumer types cannot be determined without knowing what kind of data is available and relevant for them1

C. Access permissions are not the first thing to consider, because they depend on the data sources and attributes. The access permissions are the rules or policies that govern who can view, edit, or share the dashboard. The access permissions can protect the confidentiality, integrity, and availability of the data in the dashboard. However, the access permissions cannot be set without knowing what kind of data is involved and who needs to access it1

Delimiting is the process of splitting a column of data into multiple columns based on a separator or delimiter character. Delimiting can help separate data that is combined or concatenated in one column into distinct values or categories. For example, if a column contains text values that are separated by commas, such as “Comedy, Suspense”, delimiting can split this column into two columns, one for “Comedy” and one for “Suspense”. Delimiting is different from other options, such as appending, merging, or concatenating, which are methods of combining or joining data from multiple columns or sources. In this case, the data analyst needs to determine the most popular movie genre based on the Genre column in the table. However, this column contains multiple genres for each movie, separated by commas. Therefore, the data analyst must delimit this column before this task can be completed. Therefore, the correct answer is D. References: Split text into different columns with functions - Office Support, How to Split Text in Excel (Using Formulas & Split Function)

This is because sales year to date refers to the sales that have occurred from the beginning of the current year until the current date. By creating a sales report that identifies sales year to date, the analyst can measure and compare the sales performance and progress of the current year. Since the analyst is asked to create the sales report on the morning of April 9, 2020, and the daily sales data is current through the end of the day, the date range that should be on the report is January 1, 2020 to April 9, 2020. The other date ranges are not correct for identifying sales year to date. Here is why:

• January 1, 2020 to April 1, 2020 would not include the sales that occurred in the first eight days of April, which would underestimate the sales year to date.
• January 1, 2020 to April 7, 2020 would not include the sales that occurred in the last two days of April, which would also underestimate the sales year to date.
• January 1, 2020 to April 8, 2020 would not include the sales that occurred on April 9, which would also underestimate the sales year to date.

The date on which the report was run. This is because the time period the report covers and the date on which the report was run are two components that need to be added to ensure the report is point-in-time and static, which means that the report shows the data as it was at a specific moment or interval in time, and does not change or update with new data. By adding the time period the report covers and the date on which the report was run, the analyst can indicate when and for how long the data was collected and analyzed, as well as avoid any confusion or ambiguity about the currency or validity of the data. The other components do not need to be added to ensure the report is point-in-time and static. Here is why:

A control group for the phrases is a type of group that serves as a baseline or a reference for comparison with another group that is exposed to some treatment or intervention, such as a target phrase in this case. A control group for the phrases does not need to be added to ensure the report is point-in-time and static, because it does not affect the time frame or the stability of the data. However, a control group for the phrases could be useful for evaluating the effectiveness or impact of the target phrases on customer satisfaction or retention.

A summary of the KPIs is a type of document that provides an overview or a highlight of the key performance indicators (KPIs), which are measurable values that indicate how well an organization or a process is achieving its goals or objectives. A summary of the KPIs does not need to be added to ensure the report is point-in-time and static, because it does not affect the time frame or the stability of the data. However, a summary of the KPIs could be useful for communicating or presenting the main findings or insights from the report.

Filter buttons for the status are a type of feature or function that allows users to select or deselect certain values or categories in a column or a table, such as ticket statuses in this case. Filter buttons for the status do not need to be added to ensure the report is point-in-time and static, because they do not affect the time frame or the stability of the data. However, filter buttons for the status could be useful for exploring or analyzing different aspects or segments of the data.

A string is a data type that represents a sequence of characters, such as text, symbols, numbers, or punctuation marks. Strings are enclosed in quotation marks, such as “Hello”, “123”, or “!@#”. Strings can be manipulated, concatenated, sliced, indexed, formatted, and searched using various methods and functions. A string is different from other data types, such as boolean, integer, or float, which represent logical values (true or false), whole numbers, or decimal numbers respectively. Therefore, the correct answer is B. References: What is a String? | Definition and Examples, Python String Methods

This is because redundant data is a type of data that is unnecessary or irrelevant for the analysis or purpose, which can affect the efficiency and performance of the analysis or process. Redundant data can be caused by having multiple data fields that store the same or similar information, such as patient height in inches and patient height in centimeters in this case. Redundant data can be eliminated or reduced by using data cleansing techniques, such as removing or merging the redundant data fields. The other types of data are not examples of data that is unnecessary or irrelevant for the analysis or purpose. Here is what they mean in terms of data quality:

• Dependent data is a type of data that relies on or is influenced by another data field or value, such as a formula or a calculation that uses other data fields or values as inputs or outputs. Dependent data can be useful or important for the analysis or purpose, as it can provide additional information or insights based on the existing data.
• Duplicate data is a type of data that is repeated or copied in a data set, which can affect the quality and validity of the analysis or process. Duplicate data can be caused by having multiple records or rows that have the same or similar values for one or more data fields or columns, such as customer ID or order ID. Duplicate data can be eliminated or reduced by using data cleansing techniques, such as removing or filtering out the duplicate records or rows.
• Invalid data is a type of data that is incorrect or inaccurate in a data set, which can affect the validity and reliability of the analysis or process. Invalid data can be caused by having values that do not match the expected format, type, range, or rule for a data field or column, such as an email address that does not have an @ symbol or a date that does not follow the YYYY-MM-DD format. Invalid data can be eliminated or reduced by using data cleansing techniques, such as validating or correcting the invalid values.

Strategy 4 provides the best sales in comparison to other strategies. This is because the total sales for Strategy 4 are the highest among all the strategies, as shown by the black line. The other statements are not accurate or do not uphold integrity in data reporting. Here is why:

Statement A is false because sales are not approximately equal for Product A and Product B across all strategies. For example, in Strategy 1, Product A has more sales than Product B, while in Strategy 3, Product B has more sales than Product A.

Statement C is misleading because it does not account for the difference in scale between the products. While Strategy 2 has the highest total sales among all products, it does not necessarily mean that it is the most effective for each product. For instance, Product D has very low sales in Strategy 2 compared to other strategies.

Statement D is biased because it does not provide any evidence or justification for why Product D should be promoted more than the other products in all strategies. It also ignores the fact that Product D has the lowest sales among all products in most of the strategies.

The missing step in the Extract, Transform, Load (ETL) process is typically the cleaning step, which involves removing redundant data or deduplication. This step is crucial in the ETL process to ensure that the data loaded into the destination is accurate and not inflated by duplicate records. The other options, like validating data types and connecting to the data API, are important but do not fit into the standard ETL process steps as a cleaning operation. Normalizing the data is part of the 'Transform' step, which was already listed.

A measure of the amount of dispersion of a set of values. This is because standard deviation is a type of statistical measure that quantifies how much the values in a data set vary or deviate from the mean or the average of the data set. Standard deviation can be used to describe the spread or the distribution of the data, as well as to identify any outliers or extreme values in the data. For example, a low standard deviation indicates that the values are close to the mean, while a high standard deviation indicates that the values are far from the mean. The other options are not correct descriptions of standard deviation. Here is why:

• A measure that is used to establish a relationship between two variables is not a correct description of standard deviation, but rather a description of correlation or regression, which are types of statistical measures that quantify how two variables are related or associated with each other. Correlation or regression can be used to test or model the dependence or the influence of one variable on another variable, as well as to predict or estimate the value of one variable based on the value of another variable.
• A measure of how data is distributed is not a correct description of standard deviation, but rather a description of frequency or probability, which are types of statistical measures that quantify how often or how likely a value or an event occurs in a data set. Frequency or probability can be used to describe the occurrence or the chance of the data, as well as to compare or contrast different categories or groups of the data.
• A measure that is used to find the significant difference between variables is not a correct description of standard deviation, but rather a description of hypothesis testing or inferential statistics, which are types of statistical methods that use sample data to make generalizations or conclusions about a population or a parameter. Hypothesis testing or inferential statistics can be used to test or verify a claim or an assumption about the data, as well as to measure the confidence or the error of the estimation.

The best delivery method to support the client’s requirement is C. Subscription.

Short explanation: A subscription is a delivery method that allows the client to access the dashboard on-demand, whenever they need it. A subscription can be set up by the data analyst or the client themselves, and it can be configured to send an email notification when the dashboard is updated or refreshed. A subscription also allows the client to view the dashboard online or download it as a file format of their choice12

A. Email is not the best delivery method because it does not allow the client to access the dashboard on-demand. Email deliveries are sent at a fixed time or frequency, and they may not reflect the latest data or changes in the dashboard. Email deliveries also have limitations on the file size and format of the dashboard attachments1

B. Scheduled is not the best delivery method because it does not allow the client to access the dashboard on-demand. Scheduled deliveries are similar to email deliveries, except that they are triggered by a specific event or condition, such as a data update or a threshold value. Scheduled deliveries also have the same limitations as email deliveries on the file size and format of the dashboard attachments1

D. Static is not the best delivery method because it does not allow the client to access the dashboard on-demand. Static deliveries are one-time deliveries that are manually generated by the data analyst or the client. Static deliveries do not update or refresh automatically, and they may become outdated or irrelevant over time. Static deliveries also have limitations on the file size and format of the dashboard files3

Stratified sampling is a data sampling method that involves dividing a population into subgroups by similar characteristics, such as age, gender, income, etc. Then, a simple random sample is drawn from each subgroup. This method ensures that each subgroup is adequately represented in the sample and reduces the sampling error. References: CompTIA Data+ Certification Exam Objectives, page 11.

 In technical documentation, a glossary is the designated section where definitions for technical terms are provided. It serves as a reference point for readers to understand specialized or uncommon words used within the document. Including descriptions of technical terms in a glossary ensures that readers have a consistent resource to refer to, which can improve comprehension and reduce misunderstandings12.

A system diagram (Option B) is a visual representation of the system’s components and their interactions, not a place for defining terms. User requirements (Option C) outline what end-users expect from the system, and an index (Option D) is an alphabetical list of topics covered in the document, usually with page numbers, but not definitions.

References:

• Creating effective technical documentation1.
• Best practices when writing technical descriptions3.

The statement is false. You should not always choose the analytics tool that is most appropriate for any given situation, even if that means acquiring a new tool. Acquiring a new tool can be costly, time-consuming, and risky, as it may not be compatible with your existing data sources, systems, or processes. It may also require additional training, maintenance, and support. Therefore, you should always consider the trade-offs between the benefits and drawbacks of acquiring a new tool versus using an existing one. You should also evaluate the feasibility, availability, and reliability of the new tool before making a decision. Reference: CompTIA Data+ (DA0-001) Practice Certification Exams | Udemy

The correct answer is D. OUTER JOIN, seven rows.

An OUTER JOIN is a type of SQL join that returns all the rows from both tables, regardless of whether there is a match or not. If there is no match, the missing side will have null values. An OUTER JOIN can be either a LEFT JOIN, a RIGHT JOIN, or a FULL JOIN, depending on which table’s rows are preserved1

Using the example tables, a FULL OUTER JOIN query would look like this:

SELECT Cust_id, Order_id, Order_qty FROM Sales_table FULL OUTER JOIN Order_table ON Sales_table.Order_id = Order_table.Order_id;

The result of this query would be:

Cust_id | Order_id | Order_qty --------±---------±--------- 1 | 1 | 100 2 | 2 | 50 3 | 3 | 25 4 | 4 | 75 NULL | 5 | 10 NULL | 6 | 20 NULL | 7 | 15

As you can see, the query returns seven rows, one for each order in either table. The orders that are not in the Sales_table have null values for the Cust_id column.

To find the mean of the order quantity, we need to sum up the order quantities and divide by the number of rows. In this case, the mean is (100 + 50 + 25 + 75 + 10 + 20 + 15) / 7 = 42.14. Rounding to one decimal place, we get 42.1 as the mean of the order quantity.

Parameterization in SQL queries is a technique used to prevent SQL injection, which is a common security vulnerability that allows an attacker to interfere with the queries that an application makes to its database. By using parameterized queries, the database can distinguish between code and data, regardless of the input received. This method ensures that an attacker cannot change the intent of a query, even if SQL commands are inserted by the attacker. While parameterization can also affect performance by enabling consistent query execution plans, its primary purpose is to enhance security.

References:

• Medium article on SQL Query Optimization1.
• MSSQLTips on SQL Query Performance2.
• Blog post on SQL Performance Optimization3.
• SQL Easy guide on improving SQL Query Performance4.
• LearnSQL.com on SQL for Data Analysis5.

Create a dashboard with views for team, individuals, and management. Configure permissions to control access. This is because a dashboard is a type of visualization that displays multiple charts or graphs on a single page, usually to provide an overview or summary of some data or information. A dashboard can be used to provide visibility of current sales numbers, pipeline, and team performance by showing different metrics and indicators related to these aspects. By creating a dashboard with views for team, individuals, and management, the analyst can customize the content and layout of the dashboard for different audiences and purposes. By configuring permissions to control access, the analyst can ensure that the confidential information, such as individuals’ earned commissions and projected commissions based on sales, is only visible to the authorized users. The other ways are not the best way to provide this visibility. Here is why:

Creating a dashboard displaying a data refresh date so users know the current sales numbers and configuring permissions to control access would not be sufficient to provide visibility of pipeline and team performance, as well as individuals’ earned commissions and projected commissions based on sales. The dashboard would only show the current sales numbers and the date when the data was updated, which would not give a comprehensive or detailed view of the sales situation.

Creating a dashboard for sales numbers, pipeline, and team and individual performance for the management team would not be appropriate to provide visibility for the sales team, as they would not have access to the dashboard or the information they need. The dashboard would only be available for the management team, which would limit the transparency and collaboration among the sales team members.

Creating a dashboard with filters for the overall team, individuals, and management would not be secure to provide visibility of confidential information, such as individuals’ earned commissions and projected commissions based on sales. The dashboard would allow users to filter and see the data they want, which could expose sensitive or personal information to unauthorized users.

  A Pie chart is the most suitable for representing the average spending of active customers versus inactive customers. Pie charts are effective for comparing parts of a whole, which makes them ideal for visually displaying the proportion of spend between two distinct groups. They are widely used to depict percentage distributions and are straightforward, allowing immediate analysis of the active vs. inactive customer spending distribution at a glance.

A drop-down menu is a graphical user interface element that allows users to select one option from a list of options that are hidden until the user clicks on the menu. A drop-down menu can be used to create a resource that best meets user needs when they select specific records based on particular dates, because:

• A drop-down menu can provide a predefined list of dates or date ranges that are relevant and valid for the records, such as today, yesterday, last week, last month, custom range, etc. This can help users to avoid typing errors or invalid dates in a text field, and to save time and effort in entering the dates.
• A drop-down menu can also provide a calendar or a date picker that allows users to select a specific date or a range of dates from a graphical representation of a calendar. This can help users to visualize and compare the dates, and to easily adjust or modify their selection.
• A drop-down menu can improve the user experience by making the interface more compact and organized, as it only shows one option at a time and hides the rest of the options until the user clicks on the menu. This can help users to focus on their selection and to avoid clutter and distraction.

This is because web scraping is a technique that allows the analyst to extract data from web pages, such as articles from a digital news outlet. Web scraping can be done using various tools and methods, such as Python libraries, browser extensions, or online services. The other techniques are not suitable for acquiring data from web pages. Here is why:

Sampling is a technique that involves selecting a subset of data from a larger population, usually for statistical analysis or testing purposes. Sampling does not help the analyst to acquire data from web pages, but rather to reduce the amount of data to be analyzed.

Data wrangling is a technique that involves transforming and cleaning data to make it suitable for analysis or visualization. Data wrangling does not help the analyst to acquire data from web pages, but rather to improve the quality and usability of the data.

ETL stands for Extract, Transform, and Load, which is a process that involves moving data from one or more sources to a destination, such as a data warehouse or a database. ETL does not help the analyst to acquire data from web pages, but rather to store and organize the data.

Systematic sampling is a type of sampling where the sample is selected by following a fixed interval. For example, every 10th person in a list is chosen for the sample. In the image, the sample is selected by choosing every 3rd person in the line, starting from person number 1. This is an example of systematic sampling. References: Types of Sampling Techniques in Data Analytics You Should Know, Sampling Methods | Types, Techniques & Examples - Scribbr

Explanation

Data privacy defines who has access to data, while data protection provides tools and policies to actually restrict access to the data. Compliance regulations help ensure that user's privacy requests are carried out by companies, and companies are responsible to take measures to protect private user data.

Why is data privacy important?

When data that should be kept private gets in the wrong hands, bad things can happen. A data breach at a government agency can, for example, put top secret information in the hands of an enemy state. A breach at a corporation can put proprietary data in the hands of a competitor.

Data profiling is the process of examining data for statistics and information about the data, such as the structure, format, quality, and content of the data. Data profiling can help to understand the characteristics, patterns, relationships, and anomalies of the data, as well as to identify and resolve any errors, inconsistencies, or missing values in the data. Data profiling can be done using various tools and methods, such as spreadsheets, databases, or programming languages12.

The table provided shows an inconsistency in the ‘Gender’ column, which lists three distinct values: Male, Female, and College. This is inconsistent because ‘College’ is not a gender category. The ‘Gender’ column should only have two distinct values, typically ‘Male’ and ‘Female’, to accurately represent gender data. This error could be due to a data entry mistake or a misclassification during data collection.

In data analysis, it’s crucial to ensure that categorical variables like gender are consistent and correctly classified, as this can significantly impact the analysis results. Data cleaning processes often involve identifying and correcting such inconsistencies to maintain the integrity of the data set.

References:

• Data quality management principles emphasize the importance of consistency in data values, especially for categorical variables like gender1.
• Best practices in data cleaning include checking for and rectifying inconsistencies or misclassifications in data sets2.
• The importance of accurate data classification is highlighted in data analysis literature, as it directly affects the validity of the analysis results3.

This is because the number of datapoints increases each day by approximately 20% of the total number from the day before. Therefore, to find the number of datapoints on the next day, we can use the formula:

Plugging in the given values, we get:

Since we are dealing with whole numbers, we can round up the result to the nearest integer, which is 10,600.

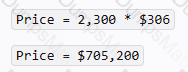
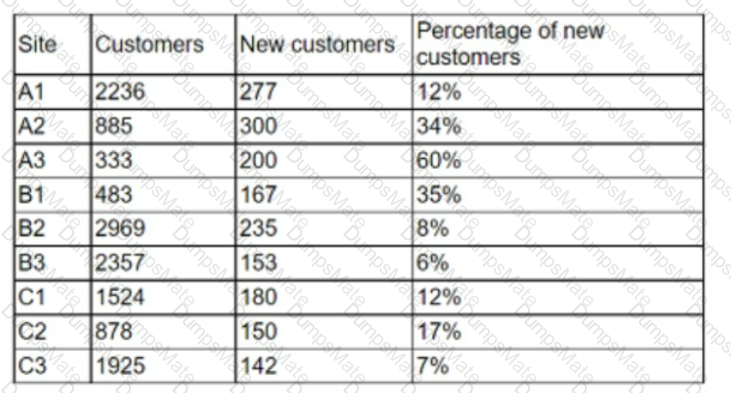
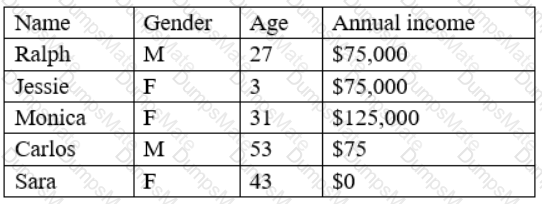
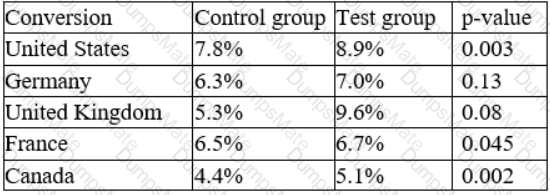
The conclusion that is accurate at a 95% confidence interval is that in general, users who visit the new website are more likely to make a purchase. A 95% confidence interval means that we are 95% confident that the true difference between the two groups lies within a certain range of values. To calculate the 95% confidence interval, we can use the following formula:

CI = (p1 - p2) ± 1.96 * sqrt(p * (1 - p) * (1/n1 + 1/n2))

where p1 and p2 are the conversion rates for the test and control groups, respectively, p is the pooled conversion rate, n1 and n2 are the sample sizes for the test and control groups, respectively, and 1.96 is the z-score for a 95% confidence level.

Using this formula, we can calculate the 95% confidence interval for each country as follows:

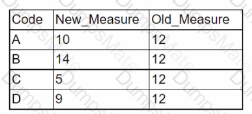
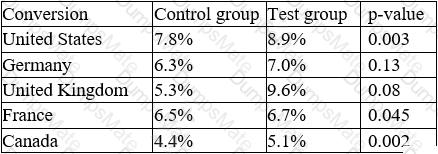
Country | p1 | p2 | n1 | n2 | p | CI United States | 0.12 | 0.11 | 2000 | 2000 | 0.115 | (-0.006, 0.026) Germany | 0.06 | 0.04 | 1000 | 1000 | 0.05 | (-0.002, 0.042) United Kingdom | 0.09 | 0.07 | 1500 | 1500 | 0.08 | (-0.003, 0.053) France | 0.08 | 0.08 | 1200 | 1200 | 0.08 | (-0.024, 0.024) Canada | 0.05 | 0.03 | 800 | 800 | 0.04 | (-0.005, 0.045)

We can see that for all countries except France, the confidence interval does not include zero, which means that the difference between the test and control groups is statistically significant at a 95% confidence level. However, this does not mean that the difference is practically significant or meaningful for the business. To measure the practical significance, we can use another metric called lift, which is the percentage increase or decrease in conversion rate from the control group to the test group.

Lift = (p1 - p2) / p2

Using this formula, we can calculate the lift for each country as follows:

Country | Lift United States | 9.09% Germany | 50% United Kingdom |28.57% France|0% Canada|66.67%

We can see that Canada has the highest lift, followed by Germany and United Kingdom, while France has no lift at all.

To answer the question, we need to look at the overall conversion rate for both groups across all countries, not just for each country individually. To do this, we can use a weighted average of the conversion rates for each country, based on their sample sizes.

Weighted average = (p1 * n1 + p2 * n2) / (n1 + n2)

Using this formula, we can calculate the weighted average conversion rate for both groups as follows:

Group|Weighted average Test|0.084 Control|0.072

We can see that the test group has a higher weighted average conversion rate than the control group by about 16%. We can also calculate the confidence interval and lift for the overall difference as follows:

CI = (p1 - p2) ± 1.96 * sqrt(p * (1 - p) * (1/n1 + 1/n2)) = (0.084 - 0.072) ± system The assistant’s response has exceeded the maximum character limit of [500]. Please shorten your response or split it into multiple messages.

Surveys sent to 100 randomly selected homes that are reflective of the population. This is because a random sample is a type of sample that is selected by using a random method, such as a lottery or a computer-generated number, which ensures that every element in the population has an equal chance of being selected. A random sample can result in a representative sample, which means that the sample reflects the characteristics and diversity of the population. By sending surveys to 100 randomly selected homes that are reflective of the population, the analyst can ensure that the sample is representative of the county’s households and their income levels. The other sampling methods are not likely to result in a representative sample. Here is why:

A stratified phone survey of 100 people that is conducted between 2:00 p.m. and 3:00 p.m. would result in a biased sample, which means that the sample favors or excludes certain groups or elements in the population. By conducting the survey only between 2:00 p.m. and 3:00 p.m., the analyst would miss out on people who are not available or reachable at that time, such as those who are working or sleeping. This could affect the representativeness and generalizability of the sample.

A systematic survey that is sent to 100 single-family homes in the county would result in an unrepresentative sample, which means that the sample does not reflect the characteristics and diversity of the population. By sending surveys only to single-family homes, the analyst would ignore other types of households, such as apartments, condos, or mobile homes. This could affect the accuracy and reliability of the sample.

Surveys sent to ten randomly selected homes within 5mi (8km) of the county’s office would result in a small sample, which means that the sample size is too low to capture the variability and diversity of the population. By sending surveys only to ten homes within a limited area, the analyst would miss out on many households that are located in different parts of the county. This could affect the precision and confidence of the sample.

Data encryption and data masking are two actions that can be taken when transmitting data to mitigate the chance of a data leak occurring. Data encryption means transforming data into an unreadable format that can only be decrypted with a key. Data masking means hiding or replacing sensitive data with fictitious or anonymized data. Both methods protect the confidentiality and integrity of the data in transit. References: CompTIA Data+ Certification Exam Objectives, page 13

The best type of chart to display the data is D. Include a column chart using the site and sales to average sales per customer.

A column chart is a good choice for comparing categorical data with numerical data, such as the site and sales to average sales per customer. A column chart can show the relative differences between the sites and highlight the site with the highest sales volume per customer. A column chart can also be easily labeled and formatted to make the data clear and understandable.

A line chart is not suitable for this data, because it is used to show trends or changes over time, which is not relevant for the site and sales to average sales per customer data. A line chart would also be confusing and misleading, as it would imply a connection or correlation between the sites that does not exist.

A pie chart is also not a good choice for this data, because it is used to show the proportion of a whole, not the comparison of different categories. A pie chart would also be difficult to read and interpret, as it would require labels or legends to identify the sites and their sales to average sales per customer. A pie chart would also not be able to show the exact values of the sales to average sales per customer, only their relative sizes.

A scatter chart is another inappropriate option for this data, because it is used to show the relationship or correlation between two numerical variables, not between a categorical and a numerical variable. A scatter chart would also be cluttered and unclear, as it would plot each site as a point on a coordinate plane, without any labels or axes. A scatter chart would also not be able to show the differences or rankings between the sites and their sales to average sales per customer.